

Up: Protokoll zur Versuchsreihe 'Röntgenstrahlen'
Previous: Compton-Effekt
Die Emission von Röntgenquanten kann - analog zum Zerfall radioaktiver
Atomkerne - als eine Folge voneinander unabhängiger Ereignisse betrachtet
werden.
Für die Häufigkeit der Zerfälle gilt bei einem radioaktiven Präparat konstanter
Aktivität die Poissonsche Verteilungsfunktion:
| P(z) |
= |
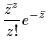 |
(8) |
Dabei ist P(z) die Wahrscheinlichkeit, zu einer beliebigen vorgegebenen
Meßdauer t genau z Ereignisse zu registrieren. 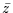 ist dabei die
mittlere Anzahl der während der Zeit t auftretenden Ereignisse.
Es wurde nun ein Intervall gewählt, in dem
ist dabei die
mittlere Anzahl der während der Zeit t auftretenden Ereignisse.
Es wurde nun ein Intervall gewählt, in dem
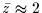 gilt, und eine
Zählstatistik von 100 Werten erstellt. Es ergab sich dabei folgende
Verteilung:
gilt, und eine
Zählstatistik von 100 Werten erstellt. Es ergab sich dabei folgende
Verteilung:
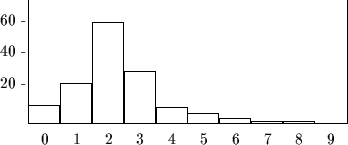 Abbildung 1: Poissonsche Häufigkeitsverteilung
Abbildung 1: Poissonsche Häufigkeitsverteilung
Vergleicht man diese experimentell ermittelten Werte mit den aus (8)
errechneten, so ergibt sich folgendes Bild:
| z |
N(z) |
P(z)experimentell |
P(z)recherisch |
| 0 |
11 |
7,2 % |
13,5 % |
| 1 |
25 |
16,4 % |
27 % |
| 2 |
63 |
41,4 % |
54 % |
| 3 |
32 |
21,0 % |
18 % |
| 4 |
10 |
6,5 % |
9 % |
| 5 |
6 |
3,9 % |
3,6 % |
| 6 |
3 |
2,0 % |
1,2 % |
| 7 |
1 |
0,6 % |
0,3 % |
| 8 |
1 |
0,6 % |
0,0 % |
| 9 |
1 |
0 % |
0.0 % |
Tabelle3: Vergleich zwischen Rechnung und Experiment.
Es zeigt sich also, daß der Wert
 offenbar nahezu erreicht wurde,
wenngleich die Steilheit der Kurve in der Praxis nicht ganz erreicht wird.
offenbar nahezu erreicht wurde,
wenngleich die Steilheit der Kurve in der Praxis nicht ganz erreicht wird.


Up: Protokoll zur Versuchsreihe 'Röntgenstrahlen'
Previous: Compton-Effekt
Tim Paehler
1998-10-30
