Theorie

Befindet sich dielektrische Materie in einem äußerem elektrischen Feld, so tritt eine Ausrichtung von Ladungen auf, was allgemein durch den Begriff der Polarisation beschrieben wird. Die Polarisation eines Mediums $\vec{P}$ wird als das gesamte elektrische Dipolmoment pro Volumen definiert.

$$\vec{P} n \cdot \vec{p}$$ = (1)

$$n \cdot \epsilon_0 \cdot \alpha \cdot \vec{E'}$$ =

Die Polarisation ist dem äußeren Feld $\vec{E}$ proportional

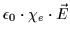$$\vec{P} \epsilon_0 \cdot \chi_e \cdot \vec{E}$$ = (2)

Das Feld am Orte des Atoms $\vec{E'}$ berechnet sich nach Lorentz zu:

$$\vec{E'} \vec{E} + \frac{1}{3 \epsilon_0} \cdot \vec{P}$$ = (3)

Damit ergibt sich aus (1):

$$\vec{P} n \cdot \alpha \cdot \epsilon_0 \cdot \vec{E'}$$ =

$$\epsilon_0 \cdot (\epsilon - 1) \cdot \vec{E} n \cdot \alpha \cdot \epsilon_0 \cdot \bigg( \vec{E} + \frac{1}{3 \epsilon_0} \cdot \epsilon_0 \cdot (\epsilon -1) \cdot \vec{E} \bigg)$$ =

$$(\epsilon - 1) n \cdot \alpha \cdot \frac{\epsilon +2}{3}$$ = (4)

und wegen $n = \frac{(m / M) \cdot N_L}{V} = \frac{\rho}{M} \cdot N_L \nonumber$

$$3 \cdot \frac{\epsilon -1}{\epsilon + 2} \cdot \frac{M}{\rho} = N_L \cdot \alpha$$ (5)

Es treten nun je nach Beschaffenheit von Material und äußerem Feld verschiedene Arten von Polarisation auf:

• Die durch die durch die Ausrichtung der permanenten Dipole hervorgerufene Orientierungspolarisation $\vec{P_O}$.
• Die durch die gegenseitige Verschiebung geladener Atome oder Atomgruppen hervorgerufene Atompolarisation $\vec{P_A}$.
• Die durch die Deformation der Elektronenwolken hervorgerufene Elektronenpolarisation $\vec{P_E}$.

Die Orientierungspolarisation $\vec{P_O}$ errechnet sich dabei aus statistischen Betrachtungen zu

$$\vec{P_O} n \cdot \epsilon_0 \cdot \alpha_0 \cdot \vec{E'}$$ = (6)

mit $\alpha_O=\frac{p_O^2}{\epsilon_0 3 k T }$.
Im allgemeinen Fall stellt die Polarisation die Summe dieser drei Polarisationsarten dar

$$\vec{P} \vec{P_E} + \vec{P_A} + \vec{P_O}$$ = (7)

$$n \cdot \epsilon_0 \cdot \alpha \cdot \vec{E'}$$ =

mit

$$\alpha \alpha_E + \alpha_A + \alpha_O$$ =

Damit erhält man aus (5) die Langevin-Debye-Beziehung:

$$3 \cdot \frac{\epsilon - 1}{\epsilon + 2} \cdot \frac{M}{\rho} N_L \cdot \bigg( \alpha_E + \alpha_A +\frac{p_O^2}{\epsilon_0 3 k T}\bigg)$$ = (8)

Betrachtet man nun statt der mittleren atomaren Polarisierbarkeit $\alpha$ die molare Polarisierbarkeit $Q=N_L \cdot \alpha$, so läßt sich diese im nach (5) wie folgt darstellen:

$$3 \cdot \frac{\epsilon - 1}{\epsilon + 2} \cdot \frac{M}{\rho}$$ Q = (9)

Im sichtbaren Spektralbereich kann man aufgrund der maxwellschen Beziehung $n^2=\epsilon$ die molare Polarisierbarkeit, die in diesem Bereich als molare Refraktion R bezeichnet wird, wie folgt darstellen:

$$3 \cdot \frac{n^2-1}{n^2+2} \cdot \frac{M}{\rho} = N_L \cdot \alpha'_E$$ R = (10)

Aufgrund der Tatsache, daß die einzelnen Polarisationskomponenten in elektrischen Wechselfeldern bei steigender Frequenz in der zu Beginn des Abschnitts aufgelisteten Reihenfolge ausgeblendet werden, läßt sich nun aus der Differenz von Q und R die molare Orientierungspolarisation errechnen. Über diese erhält man damit die folgende Formel für das Dipolmoment einer mit dem Molenbruch x₁ verdünnten Lösung:

$$\sqrt{\epsilon_0 \cdot 3 k T \cdot (\bar{Q} - \bar{R}) / (x_1 \cdot N_L)}$$ p_O = (11)