


Next: Verallgemeinerung auf beliebige Anzahlen
Up: Wahrscheinlichkeiten bei Entscheidungsfindungen
Previous: Wahrscheinlichkeiten bei Entscheidungsfindungen
Wahrscheinlichkeiten werden im allgemeinen so normiert, daß sie durch
eine Zahl zwischen 0 und 1 beschrieben werden. Ein Ereignis mit der
Wahrscheinlichkeit von 1 (
 )
tritt dabei mit absoluter
Sicherheit auf, eines mit der Wahrscheinlichkeit 0 auf keinen Fall.
Damit ließe sich die Wahrscheinlichkeit für ein ``richtiges'' Urteil bei
einem Geschworenen, der zu
)
tritt dabei mit absoluter
Sicherheit auf, eines mit der Wahrscheinlichkeit 0 auf keinen Fall.
Damit ließe sich die Wahrscheinlichkeit für ein ``richtiges'' Urteil bei
einem Geschworenen, der zu  eine richtige Entscheidung
eine richtige Entscheidung  fällt,
mit
fällt,
mit
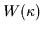 |
= |
0,7 |
(1) |
beschreiben.
Wahrscheinlichkeiten zweier (und mehrerer) Ereignisse, die voneinander
unabhängig sind, multiplizieren sich miteinander. Da dies für Geschworene
der Fall sein sollte, gilt z.B. bei der Erhöhung der Anzahl der
Geschworenen auf 2 für die Wahrscheinlichkeit eines richtigen Urteils:
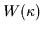 |
= |
0,72 |
(2) |
| |
= |
0,49 |
(3) |
Sie ist also zunächst kleiner, da von den vier Möglichkeiten der Entscheidung
nur eine (nämlich die, daß beide Geschworenen richtig urteilen) zum Erfolg
führt.
Diese Unregelmäßigkeit verschwindet jedoch im allgemeinen Fall der
Erhöhung der Anzahl der Geschworenen, wenn man voraussetzt, daß keine
einstimmige Entscheidung, sondern lediglich eine Mehrheitsentscheidung
für die Urteilsfindung notwendig ist. So hätte man bei drei Geschworenen
a, b, c folgende Möglichkeiten der Entscheidungsverteilung bei den
Individuen:
| Nr. |
a |
b |
c |
Gemeinsames Urteil |
| 1 |
f |
f |
f |
f |
| 2 |
f |
f |
r |
f |
| 3 |
f |
r |
f |
f |
| 4 |
r |
f |
f |
f |
| 5 |
f |
r |
r |
r |
| 6 |
r |
f |
r |
r |
| 7 |
r |
r |
f |
r |
| 8 |
r |
r |
r |
r |
Man erkennt, daß eine gleiche Anzahl von wahren und falschen
Entscheidungsmöglichkeiten vorliegt. Wären also alle Einzelentscheidungen
gleichwahrscheinlich, so erhielte man eine Gesamtwahrscheinlichkeit
von (Anzahl der günstigen Fälle/Anzahl der möglichen Fälle = ) 50%.
Berücksichtigt man aber zusätzlich die Wahrscheinlichkeit der
Einzelentscheidung von 0,7 für eine richtige Entscheidung und 0,3
für eine falsche Entscheidung, so ergibt sich ein anderes Bild:
| Nr. |
a |
b |
c |
Wahrscheinlichkeit |
| 1 |
f |
f |
f |
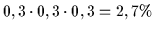 |
| 2 |
f |
f |
r |
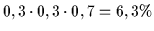 |
| 3 |
f |
r |
f |
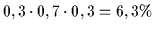 |
| 4 |
r |
f |
f |
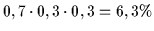 |
| 5 |
f |
r |
r |
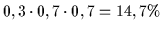 |
| 6 |
r |
f |
r |
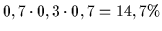 |
| 7 |
r |
r |
f |
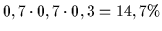 |
| 8 |
r |
r |
r |
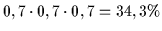 |
Summiert man die Wahrscheinlichkeiten auf, so ergibt sich eine
Gesamtwahrscheinlichkeit von  für ein richtiges Urteil bzw.
für ein richtiges Urteil bzw.
 für eine falsche Entscheidung, was gegenüber der Entscheidung
eines einzelnen Geschworenen bereits einen Zuwachs an Sicherheit bedeutet.
Wichtig zu bemerken ist dabei vor allem,
daß der Fall, in dem 2 Geschworene richtig und einer falsch votieren
(unabhängig davon, welche), mit
für eine falsche Entscheidung, was gegenüber der Entscheidung
eines einzelnen Geschworenen bereits einen Zuwachs an Sicherheit bedeutet.
Wichtig zu bemerken ist dabei vor allem,
daß der Fall, in dem 2 Geschworene richtig und einer falsch votieren
(unabhängig davon, welche), mit
 wahrscheinlicher
ist als der, daß alle richtig stimmen, daß also einzelne Kombinationen durch
mehrfaches Auftreten wahrscheinlicher sind als andere, die nur einfach
möglich sind1. Die Menge aller Kombinationen zu einem solchen
Fall nennt man die Komposition. Da es für das Ergebnis unerheblich ist,
welcher Geschworene im einzelnen welches Urteil gefällt hat, berechnet man im
allgemeinen direkt die Wahrscheinlichkeit einer Komposition.
wahrscheinlicher
ist als der, daß alle richtig stimmen, daß also einzelne Kombinationen durch
mehrfaches Auftreten wahrscheinlicher sind als andere, die nur einfach
möglich sind1. Die Menge aller Kombinationen zu einem solchen
Fall nennt man die Komposition. Da es für das Ergebnis unerheblich ist,
welcher Geschworene im einzelnen welches Urteil gefällt hat, berechnet man im
allgemeinen direkt die Wahrscheinlichkeit einer Komposition.



Next: Verallgemeinerung auf beliebige Anzahlen
Up: Wahrscheinlichkeiten bei Entscheidungsfindungen
Previous: Wahrscheinlichkeiten bei Entscheidungsfindungen
Tim Paehler
1998-10-30